El papel de la religión en el desarrollo de las ciencias matemáticas en la civilización islámica medieval

Por el Prof. Nuh Aydin, Profesor de Matemáticas, Kenyon College

 

El surgimiento de la civilización islámica fue uno de los principales acontecimientos de la historia mundial. Un aspecto importante de la civilización islámica medieval fue el desarrollo de una notable tradición científica en un período de tiempo relativamente corto. Fue el hogar de la producción científica más avanzada de su tiempo durante varios siglos. Hubo muchos factores detrás de este desarrollo y la religión del Islam fue uno de los factores clave. En este artículo, examinamos cómo la fe y la práctica islámicas llevaron al desarrollo de las ciencias en general y las ciencias matemáticas en particular en el mundo islámico medieval.

Introducción

Solo aproximadamente un siglo después de su nacimiento, el Islam se extendió por una gran región desde España hasta las fronteras de India y China y se desarrolló una civilización notable. Un aspecto de esta civilización fue que se convirtió en el centro de aprendizaje, erudición e investigación científica en un período de tiempo relativamente corto. Existen algunas diferencias entre los historiadores de la ciencia al evaluar el papel de la ciencia islámica medieval en términos de su duración (el período a menudo denominado «la edad de oro de la ciencia islámica»), su importancia en el contexto del desarrollo de la ciencia moderna y su influencia en otras culturas y civilizaciones, en particular el Renacimiento europeo (compárese, por ejemplo, con Arnold & Alfred 1931 y Saliba 2007). Aún así, existe un acuerdo general de que la civilización islámica fue el hogar de la ciencia más avanzada durante algunos siglos (ya sea del siglo IX al XII o del siglo IX al XVI o XVII). Ver (Saliba, 2007) para una discusión detallada de las dos narrativas sobre la historia y la importancia de la ciencia islámica.

Nos gustaría aclarar los términos «ciencia islámica» y «civilización islámica». Usaremos los términos «civilización islámica» y «civilización islámica medieval» en un sentido muy amplio. Nos referimos particularmente a la civilización islámica medieval cuyo período de tiempo se extiende aproximadamente desde finales del siglo VII hasta el siglo XVI (inclusive). Geográficamente, se extiende por una gran región, desde España en el oeste hasta China e India en el este. Por lo tanto, abarca mucha diversidad en términos de idiomas, etnias y culturas. También contiene muchos poderes políticos y organizaciones diferentes (como omeyas, abasíes, fatimíes, al-Andalus, selyúcidas, otomanos, safávidas y otros). Era muy diversa desde el punto de vista étnico y religioso, en la que personas de diferentes orígenes contribuyeron al progreso y al conocimiento científico, ser musulmán no era un requisito previo para esta contribución. El árabe fue el idioma de la ciencia durante este período y ha sido el idioma de los estudios religiosos. Usamos el término en un sentido muy amplio y de ninguna manera implicamos una cultura o civilización monolítica.

Con el término «ciencia islámica» nos referimos a trabajos científicos producidos en la civilización islámica como se explicó anteriormente. Las personas que participaron en la producción de esta ciencia no eran todas musulmanas, aunque la mayoría lo eran, y ciertamente no todas eran árabes, aunque el árabe era el idioma utilizado la mayor parte del tiempo. En particular, este término no se refiere a las ciencias religiosas en el Islam como tafsir, hadiz, fiqh, etc.

Como se explica en (Saliba 2007, Capítulo 2), el rápido aumento de las actividades científicas en la civilización islámica fue la consecuencia de muchos factores, como los políticos, económicos, sociales y religiosos. No se puede explicar por un solo factor. El propósito de este artículo es examinar uno de estos factores en el surgimiento de las ciencias, particularmente las ciencias matemáticas, en la civilización islámica temprana: el papel de la religión del Islam. Podemos ver que hay dos formas principales en las que el Islam tuvo un impacto directo en las actividades científicas.

1. El estímulo general del Islam sobre el razonamiento, la adquisición de conocimientos y el estudio de la naturaleza.
2. El cumplimiento de ciertas obligaciones religiosas que requieren cálculos matemáticos.

En el resto del artículo, explicaremos y ampliaremos estos dos puntos.

El fomento de la fe islámica para la investigación científica

La religión del Islam pone mucho énfasis en el pensamiento racional, el razonamiento, el aprendizaje, la búsqueda de conocimiento y el estudio de la naturaleza como un signo de la creación y el poder de Dios. Podemos ver una gran cantidad de referencias a estos puntos en la fuente principal de religión del Islam: el Corán. El Corán anima encarecidamente a los seres humanos a utilizar su capacidad intelectual y contemplar todo tipo de fenómenos del mundo natural, desde los movimientos del sol y la luna hasta los beneficios de la miel. De manera similar, los dichos del profeta Muhammad, llamados hadices por la tradición islámica, que es la segunda fuente de religión en el Islam, contienen muchos ejemplos que enfatizan el valor de buscar el conocimiento. Damos algunos ejemplos de los versículos del Corán y hadices sobre el tema.

Versos del Corán

Los primeros versículos del Corán que le fueron revelados al Profeta Muhammad tenían que ver con el aprendizaje y la enseñanza.

¡Lee! [¡oh, Muhammad!] En el nombre de tu Señor, Quien creó todas las cosas. Creó al hombre de una célula embrionaria. ¡Lee! Que tu Señor es el más Generoso. Enseñó la escritura con la pluma y le enseñó al hombre lo que este no sabía. (Corán, 96: 1-5)

Es realmente interesante y significativo notar que la palabra árabe para el término verso (آية plural آيا ت) se refiere tanto a los versos del Corán como a los signos que Dios colocó en el universo para que los seres humanos pensaran. Por lo tanto, el comando «lee» puede entenderse como leer los versículos del Corán y leer los signos del universo. Ambos tipos de lectura requieren un esfuerzo intelectual. El siguiente versículo hace este punto.

Así es como aclaro los signos para quienes razonan. (Corán, 30:28)

El idioma árabe se basa en el sistema raíz. Casi todas las palabras árabes (con pocas excepciones) tienen una raíz de 3 letras de la que se puede derivar una gran cantidad de palabras relacionadas. El significado esencial de la raíz impregna todas las palabras derivadas de ella. Hay 49 versículos en el Corán (corpus.quran.com) que contienen palabras derivadas de la raíz ع ق ل (a’- qa-la) que significa razonar, usar el intelecto, comprender y entender. A continuación se muestran tres ejemplos de estos versículos.

Así es como Dios evidencia Sus preceptos para que usen la razón. (Corán, 2: 242).

Él es Quien los creó del polvo, y después de un óvulo fecundado que se transforma en un embrión, luego los hace surgir [al mundo] como niños para que alcancen la madurez, y luego los hace llegar a ancianos, aunque algunos fallecen antes, y así se cumple el plazo de vida que se les había prefijado para que usen la razón. (Corán, 40:67)

Sepan que Dios da vida a la tierra árida. Les explico estos signos para que entiendan. (Corán, 57:17)

La raíz ف ك ر (fa-ka-ra) contiene el significado de reflexionar y contemplar. Hay 18 versículos en el Corán que contienen palabras de esta raíz. A continuación se muestran algunos ejemplos:

Diles: “No les digo que poseo los tesoros de Dios ni que conozco lo oculto, ni tampoco afirmo ser un ángel, solo sigo lo que me fue revelado”. Diles: “¿Acaso pueden equipararse el ciego y el vidente? ¿Acaso no van a reflexionar?” (Corán, 6:50)

Aliméntense de los frutos y transiten por donde les ha facilitado su Señor”. De su abdomen sale un jarabe de diferentes colores que es medicina para la gente. En esto hay un signo para quienes reflexionan. (Corán, 16:69)

Además de los dos ejemplos anteriores, hay muchas otras palabras que contienen el significado de «conocer», «comprender», «informar», «ver», «observar», «considerar», «juzgar», «considerar apropiado», «cuestionar”, “indagar”, “probar”, “justificar”, “aclarar”, “explicar”, “dar a conocer”, “determinar” y “medir”. Por ejemplo, las palabras derivadas de la raíz ع ل م (a’- li-ma: saber) aparecen en el Corán 854 veces, de ر ا ي (ra-a-ya: ver, percibir, notar, observar, discernir, juzgar, ser de la opinión, considerar apropiado) 328 veces, de س أ ل (se-a-le: preguntar, cuestionar) 129 veces, de ن ب ا (na-ba-a: informar) 160 veces, de ح ك م (ha-ka-ma: juzgar) 210 veces, de ح س ب (ha-sa-be: pensar, tomar algo en cuenta) 109 veces, de ف ق ه (fa-qa-ha: entender, comprender) 20 veces, de ح ق ق (ha-qa-qa: probar, justificar, comprobar) 287 veces, de ب ي ن (ba-ya-na: aclarar, explicar, demostrar) 257 veces, de دري (da-ra-ya: dar a conocer) 29 veces, de ف ص ل (fa-sa -la: aclarar, explicar en detalle) 43 veces, de ق د ر (qa-da-ra: determinar, medir, evaluar) 132 veces, de ص ر ف (sa-ra-fa: explicar) 30 veces.

Además, hay muchos versículos en el Corán que animan a los seres humanos a estudiar la naturaleza como creación de Dios y la manifestación de Su poder y atributos. Estos versículos también llaman la atención sobre el hecho de que hay un orden y equilibrio en el universo y el movimiento de los cuerpos celestes que se realiza mediante cálculos matemáticos precisos. Aquí están algunos ejemplos

En la creación de los cielos y de la Tierra, y en la sucesión de la noche y el día, hay signos para los dotados de intelecto. (Corán, 3: 190)

¿Acaso no reflexionan [los que niegan la verdad] en la maravillosa creación del camello? En el cielo, cómo ha sido elevado. En las montañas, cómo han sido afirmadas. Y en la Tierra, cómo ha sido extendida. (Corán, 88: 17-20)

El Sol y la Luna siguen una órbita precisa (Corán, 55: 5)

Y levantó el cielo e impuso la balanza. (Corán, 55: 7)

Terminamos esta sección con algunos versículos que capturan la idea general que intentamos resaltar.

Dios concede la sabiduría a quien quiere, y sepan que a quien le haya sido concedido este don ha recibido una gracia inmensa. Solo reflexionan los dotados de intelecto. (Corán, 2: 269).

Dile: «¿Acaso son iguales los que tienen conocimiento y los que no tienen conocimiento?» Solo reflexionan los dotados de entendimiento. (Corán, 39: 9).

«Mi Señor, acrecienta mi conocimiento». (Corán, 20: 114)

Dichos del Profeta (Hadices) sobre el aprendizaje

Los dichos del profeta Muhammad, llamados hadices en la tradición islámica, son una fuente importante de religión en el Islam, en segundo lugar después del Corán. De hecho, la ciencia del hadiz es una de las principales ramas de las disciplinas teológicas en el Islam. Hay una serie de hadices auténticos del profeta que fomentan el aprendizaje. A continuación se muestra una selección de hadices sobre el tema. El primer hadiz de la lista establece claramente que es obligatorio para todo musulmán, hombre o mujer, buscar conocimiento.

Buscar el conocimiento es un deber de todo musulmán, hombre o mujer (Sunan Ibn Mayah, The Book of the Sunnah, 224)

Quien salga en busca de conocimiento, estará en la causa de Dios hasta que regrese (Jami at-Tirmidhi, The Book of Knowledge, 2647).

La palabra de sabiduría es propiedad perdida del creyente, así que dondequiera que la encuentre, tiene un mejor derecho a ella (Jami at-Tirmidhi, The Book of Knowledge, 2687).

Dios me ha revelado: A quien camina en la búsqueda del conocimiento le facilito el camino al cielo. (Jami at-Tirmidhi, El libro del conocimiento, 2646; Riyad as-Salihin, El libro del conocimiento, 1381)

No desees ser como nadie excepto en dos casos. (El primero es) Una persona a quien Dios le ha dado riquezas y las gasta con justicia; (el segundo es) aquel a quien Dios le ha dado sabiduría y actúa de acuerdo con ella y la enseña a otros (Sahih al-Bujari, Libro 3, Hadiz 15)

Los eruditos son los herederos de los profetas; dejan el conocimiento como herencia; quien la hereda hereda una gran fortuna (Riyad as-Salihin, The Book of Knowledge, 1388)

La superioridad del sabio sobre el devoto adorador es como la de la luna llena sobre el resto de las estrellas (en brillo) (Riyad as-Salihin, The Book of Knowledge, 1388)

Es mejor meditar profundamente durante una hora que un año de adoración (mecánica/voluntaria) (Suyutî, Camiu’s-sağir, 2/127; Aclûnî, I / 310)

No hay ninguna enfermedad que Dios haya creado, sin que Él también haya creado su tratamiento (Sunan Ibn Mayah, The Book of Medicine, 3438).

Ten en cuenta que el último hadiz mencionado anteriormente es un gran estímulo para la investigación en medicina. Quizás, el más famoso de todos los científicos de la civilización islámica es Ibn Sina (980-1037), también conocido como Avicena en Occidente. Es conocido por su investigación en medicina y filosofía. Su libro médico autorizado The Canon of Medicine (القانون في الطب en árabe) fue un libro de texto estándar en las universidades europeas hasta mediados del siglo XVII (al-Khalili, 2010). Muchos historiadores de la ciencia reconocen la importancia y la influencia del Canon. Por ejemplo, «Probablemente ningún trabajo médico que se haya escrito jamás ha sido tan estudiado», dice Meyerhof en (Arnold & Alfred 1931).

Los primeros eruditos musulmanes tomaron en serio este consejo de buscar conocimiento y lo practicaron lo mejor que pudieron. Buscaron conocimiento dondequiera que estuviera disponible. Viajaron grandes distancias para adquirir sabiduría y el legado de civilizaciones anteriores que produjeron las ciencias más avanzadas de la época. No dudaron en recibir ciencia desde el griego antiguo, que fue abandonado y perseguido bajo el dominio bizantino, hasta la India. Un ejemplo excelente que muestra un resultado fructífero de la síntesis del conocimiento que los eruditos musulmanes adquirieron de griegos e indios es la creación de la disciplina del álgebra que fue iniciada por al-Juarizmi (780-850) a principios del siglo IX en Bagdad, en la casa de la sabiduría bajo el patrocinio del califa al-Ma’mun (reinó 813-833). En su libro, Kitab al-jabr wa’l muqabala al-Juarizmi combinó el enfoque griego de las matemáticas que era esencialmente geométrico con la herencia babilónica e india de sistemas numéricos eficientes para crear una nueva ciencia del álgebra. Muchos estudiosos de la civilización islámica contribuyeron al desarrollo del álgebra en los siglos posteriores a al-Juarizmi. Hoy, el álgebra es una de las principales ramas de las matemáticas modernas. No solo es una disciplina importante por derecho propio, sino que también influyó prácticamente en todas las ramas de las matemáticas modernas, como lo demuestra el hecho de que muchos subcampos de las matemáticas modernas incluyen el adjetivo «algebraico» en su título, como la teoría de números algebraica, geometría algebraica, topología algebraica, etc.

Las ciencias matemáticas desarrolladas como respuesta a los requisitos de la práctica religiosa

Lo que hemos discutido hasta ahora establece una base filosófica y teológica en el Islam para emprender actividades científicas. Resulta que el Islam no se detuvo en el nivel filosófico para animar a la gente a aprender. También brindó a sus seguidores desafíos prácticos que solo podrían resolverse produciendo nuevos conocimientos. Hay muchas obligaciones religiosas en el Islam cuya práctica requiere cálculos matemáticos, a veces muy sofisticados. Muchos de estos problemas eran problemas completamente nuevos que las civilizaciones anteriores no enfrentaron. Por lo tanto, los eruditos musulmanes necesitaban encontrar soluciones novedosas para ellos. Esta fue una de las formas directas y concretas en las que la religión jugó un papel importante en el rápido desarrollo de las ciencias en la civilización islámica primitiva. Los académicos se esforzaron por resolver estos problemas utilizando el conocimiento disponible de la época y, en muchos casos, creando nuevos conocimientos y herramientas matemáticas. En sus voluminosos tres volúmenes de In Synchrony with the Heavens, David King examina la relación entre los requisitos religiosos y la creación de nueva ciencia para satisfacer esos requisitos basándose en fuentes originales. Afirma que “El material presentado aquí hace que la noción moderna popular de que la religión obstaculice inevitablemente el progreso científico sea un sinsentido, porque en este caso, los requisitos de la primera inspiraron a la segunda durante siglos” (King 2004, p. Xvii).

Observamos algunos ejemplos de estos problemas en esta sección:

El tiempo para la oración

Uno de los cinco pilares del Islam son las cinco oraciones diarias (salat) que deben realizarse durante ciertos períodos del día. Estos períodos de tiempo están determinados por la posición del sol y cambian por la ubicación en la Tierra y las estaciones del año. Por lo tanto, deben calcularse para cada día del año y para cada lugar de la Tierra. Este es entonces un problema astronómico que también involucra geografía y matemática. Hoy en día, existen dispositivos electrónicos y calculadoras en línea que calculan los tiempos de oración diarios para todos los lugares de la Tierra y para todos los días del año para los musulmanes practicantes (por ejemplo, www.islamicfinder.org). Tradicionalmente, esta necesidad se ha satisfecho con mesas de oración preparadas para cada lugar por astrónomos competentes. En (King 2004) se presenta un gran número de estos cuadros. La solución de este problema no trivial llevó a la creación de una disciplina científica en el Islam llamada ilm al-miqat (عِلم الْمِيقات), la ciencia del cronometraje. También condujo al surgimiento de una clase profesional llamada muwaqqits (literalmente «cronometradores») que eran astrónomos especializados en la determinación de los tiempos de oración diarios. Nacidos en Egipto y Siria en el siglo XIII (King 2004), los muwaqqits estaban asociados con una mezquita en particular. Quizás el más famoso de estos muwaqqits es Ibn al-Shatir (1304-1375), quien estuvo asociado con la mezquita omeya en Damasco. Aparte de su deber oficial de cronometraje, produjo algunos de los trabajos más avanzados de astronomía teórica de su tiempo mientras trabajaba en la resolución de problemas cosmológicos en el Almagesto de Ptolomeo. Los investigadores descubrieron a mediados del siglo XX que su trabajo influyó directamente en la astronomía de Copérnico (Roberts, 1957; Saliba 2007). Esta notable conexión aún no es ampliamente conocida, no solo entre el público educado sino también entre los historiadores de la ciencia.

La definición de los intervalos para las cinco oraciones musulmanas se basa en ciertos versículos del Corán y los hadices y la práctica del profeta Muhammad. El profeta Muhammad vivió en las ciudades de La Meca y Medina, que están cerca del ecuador. A medida que el Islam se extendió mucho más al norte en un corto período después del profeta, aparecieron algunos problemas interesantes en la determinación de ciertos tiempos de oración debido a la ubicación. Por ejemplo, el criterio para la determinación de la oración de la tarde (aasr) que se practicaba en La Meca y Medina no podía utilizarse en lugares como Damasco en determinadas épocas del año porque la longitud de la sombra de un objeto nunca es tan corta como su duración durante muchos días del año. Los académicos respondieron estableciendo nuevos criterios para tales casos. El problema estaba directamente relacionado con la trigonometría. Los eruditos musulmanes definieron las funciones trigonométricas de tangente y cotangente en términos de sombras, como la relación entre la longitud de un gnomon y la longitud de su sombra (Berggen 1986). Después de los trabajos de los eruditos musulmanes, quedaba poco por descubrir en el campo de la trigonometría (Saliba 2007, p. 187).

El día comienza con la puesta del sol en el calendario islámico. La puesta del sol es el comienzo del período de la oración vespertina, al-maghrib, que dura hasta el anochecer cuando comienza el intervalo para la siguiente oración al-isha, la cual dura hasta el amanecer. La oración de la mañana, al-fayr, debe realizarse entre el alba y el amanecer. La siguiente oración, al-duhr, comienza poco después del mediodía (cuando el sol cruza el meridiano) y dura hasta que la longitud de la sombra de un objeto es igual a la longitud del objeto (o la longitud de la sombra al mediodía más la longitud del objeto). La última oración del día, al-aasr, comienza al final del período del duhr y termina cuando la longitud de la sombra es igual al doble de la longitud del objeto (o la longitud de la sombra al mediodía más el doble la longitud del objeto).

La siguiente figura da una idea general sobre los períodos de tiempo específicos para las oraciones diarias musulmanas. Tenga en cuenta que existen variaciones significativas en la duración de cada período de tiempo según la época del año y la ubicación en la tierra.

Uno de los eruditos islámicos medievales que escribió sobre las sombras, su utilidad en la determinación de los tiempos de oración diarios y las definiciones de funciones trigonométricas es el erudito del siglo XI de Asia central: Abu al-Raihan Muhammad b. Ahmad al-Biruni (973-1048). Su tratado de sombras es editado, traducido y comentado por E. S. Kennedy (Kennedy 1976). La determinación de los tiempos de oración fue un problema completamente nuevo para la comunidad musulmana que las civilizaciones anteriores no encontraron.

El problema de la alquibla

Otro requisito para un musulmán practicante relacionado con las oraciones diarias es orientarse mirando a la Ka’ba, ubicada en La Meca. Esta es la mezquita más sagrada de la tradición islámica. Inicialmente, los musulmanes se orientaban mirando al Noble Santuario en Jerusalén durante más de 13 años en sus oraciones, luego un verso le fue revelado al Profeta Muhammad durante una oración que le indicaba que se orientara a la Kaaba a partir de este momento (Corán, 2; 144). La alquibla se refiere a la dirección, relativa a una localidad determinada, a la que uno debe orientarse al realizar las oraciones musulmanas. Para los lugares cercanos a La Meca, la determinación de la alquibla era un problema relativamente sencillo. A medida que el Islam se extendió en muchas direcciones, determinar la alquibla desde lugares lejanos se volvió más difícil y el problema de la alquibla resultó ser un problema interesante con aspectos religiosos, científicos y sociales. A medida que aumentaba el conocimiento de la astronomía, los estudiosos se dieron cuenta de que se necesitaba geometría esférica para resolver el problema con precisión en lugares alejados de La Meca. Se dieron cuenta de que algunas mezquitas construidas en períodos anteriores del Islam estaban desalineadas, en algunos casos en un grado significativo. Qué hacer con tales mezquitas y qué método para determinar la alquibla usar fue tema de un serio debate entre los eruditos islámicos (Dallal, 2010). Algunos eruditos religiosos argumentaron que no se debería exigir el uso de técnicas matemáticas sofisticadas para determinar la alquibla porque solo unas pocas personas pueden obtener tal conocimiento que es contrario al espíritu del Islam (Dallal, 2010). Sin embargo, esto no puso fin al debate. Los académicos con conocimientos astronómicos avanzados continuaron trabajando en el problema y desarrollaron varias técnicas matemáticas para resolverlo.

En última instancia, la solución del problema de la alquibla requiere una trigonometría esférica no trivial porque la Tierra es una esfera (aproximadamente). A pequeña escala, está bien suponer que la Tierra es una superficie plana, pero en distancias mayores es necesario utilizar círculos máximos para resolver el problema (consulte la Figura 3 a continuación). El conocimiento avanzado de trigonometría esférica que se necesitaba no estaba disponible en civilizaciones anteriores, por lo que los eruditos musulmanes desarrollaron este material. Según Berggren, hay tres astrónomos que fueron responsables de desarrollar resultados importantes en trigonometría esférica: Habash al-Hasib (m. Después de 869), Abu’l-Wafa Al-Buzjani (940-998) y Abu Nasr Mansur ibn Ali ibn. Irak (970-1036) (Berggren, 2003). Un resultado clave que fue útil para resolver el problema de la alquibla fue el descubrimiento de la ley de los senos para triángulos esféricos derivada de Abu’l-Wafa.

Uno de los grandes científicos musulmanes que trabajó en el problema de la alquibla es Al-Biruni (973-1048), un verdadero erudito que presentó cuatro métodos para resolverlo (Berggren, 2003). Se puede encontrar un resumen de su solución en (Berggren, 2003). Otro enfoque al problema fue la composición de tablas que muestran la alquibla para un conjunto de localidades, similar a las tablas de tiempos de oración. Muhammad al-Jalili, un muwaqqit del siglo XIV, proporcionó un gran ejemplo de tal tabla, que contenía 2880 entradas, es decir, mostraba la alquibla para 2880 ubicaciones diferentes (Berggren, 2003).

La determinación de los meses lunares y la visibilidad de la luna creciente

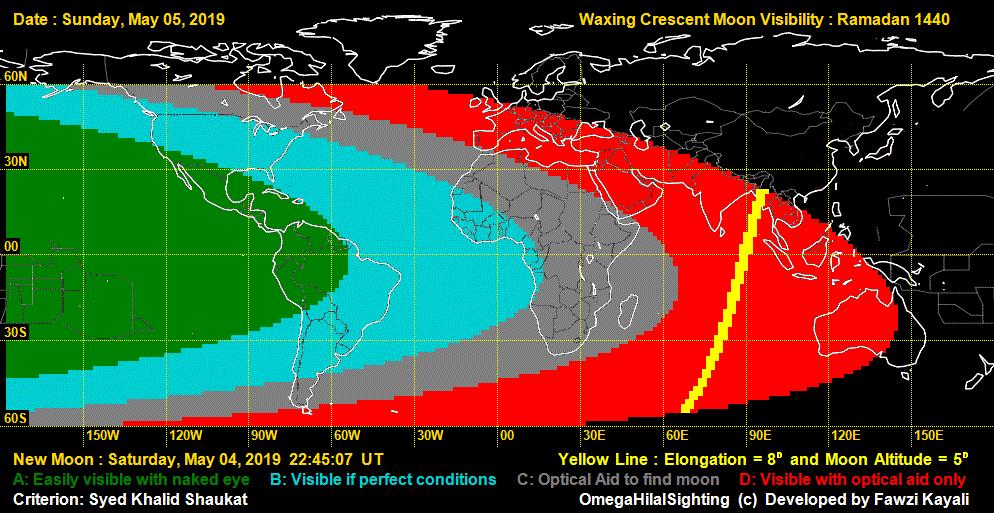
El calendario islámico es un calendario estrictamente lunar, por lo tanto, los principales días religiosos en el Islam se determinan en los ciclos de la luna, como el comienzo y el final del mes sagrado de Ramadán, los dos Eids y la peregrinación. Un nuevo mes comienza con una nueva luna creciente. La duración media de un mes lunar es de aproximadamente 29,5 días, por lo que algunos meses lunares son de 29 días, otros 30. Inicialmente, la comunidad musulmana determinaba los meses lunares basándose en la observación a simple vista. Cuando las nubes hacían imposible observar la luna nueva, completaban el mes anterior a 30 días. A medida que avanzaba la ciencia de la astronomía, los eruditos musulmanes también prestaron atención a los cálculos de los meses lunares. Dado que la visibilidad de la luna varía según la ubicación de la Tierra, todavía existen desacuerdos entre los musulmanes de hoy a pesar de la disponibilidad de las herramientas de la ciencia y la tecnología modernas. Se incluye el siguiente mapa para que el lector se haga una idea de la complejidad del problema. El mapa es accedido desde http://moonsighting.com.

El cálculo del Zakat y de la herencia

Uno de los pilares del Islam es el zakat, la participación de la comunidad en la riqueza privada. Se paga sobre la riqueza acumulada más allá de las necesidades básicas. La tasa del zakat varía entre el 2,5% (1/40) y el 20% (1/5) según el tipo de activo. Es del 2,5% sobre el dinero y los activos de capital. El zakat se menciona en más de treinta versículos del Corán. Claramente, se necesita un conocimiento básico de aritmética de fracciones para los cálculos del zakat.

Otra área de la ley islámica que requiere aritmética básica son los cálculos de las participaciones legales en herencias y legados. Dependiendo de la situación, estos problemas pueden complicarse. Los cálculos de estos porcentajes surgieron como una nueva ciencia en el Islam llamada ilm al-faraid, la ciencia de las obligaciones, que es tanto una ciencia religiosa (jurisprudencia) basada en los versos del Corán y los hadices, como una ciencia matemática. Esta ciencia de ilm al-faraid tiene una conexión interesante con el comienzo del álgebra.

Al-Juarizmi (780-850) escribió el primer libro de álgebra de la historia Kitab al-jabr wa-al-muqabala alrededor del año 820 en Bagdad. El texto original de su libro junto con la traducción al inglés y los comentarios están disponibles (Rasshed, 2009). Al comienzo del libro, Al-Juarizmi explica su motivación para escribirlo. Dice que el califa al-Ma’mun (813-833) lo animó a escribir un libro conciso sobre la forma de cálculo en álgebra y al-muqabala.

…Quería incluir lo que es sutil en el cálculo y lo que es más noble en él y lo que la gente necesita en materia de sus herencias, sus legados, sus juicios, sus transacciones comerciales y todo lo que tratan en el cuestión de topografía de parcelas de Tierra, excavación de canales de agua, medición y otras cosas relacionadas con el cálculo…

Afirma claramente que una de las motivaciones de la nueva ciencia del álgebra que presenta es ayudar a las personas con sus cálculos del zakat y herencia. De hecho, aproximadamente la mitad de su libro es el Libro de testamentos (Kitab al-wasaya) en el que analiza muchos ejemplos de problemas de herencia y legado. Puede resultar sorprendente que una parte tan grande del primer libro de álgebra de la historia esté dedicada a los problemas de la herencia y el legado. Una breve explicación del contexto histórico puede arrojar algo de luz sobre por qué ese es el caso, como se explica en (Rasshed, 2009).

El siglo VIII fue el momento en que se establecieron las bases de tres de las cuatro principales escuelas de derecho del Islam sunita: Hanafi, Maliki y Shafi. Un elemento de la ley islámica eran las reglas de herencia, testamentos y legados. Por eso, los juristas de la época escribieron muchos libros sobre el tema. Algunos de estos juristas desarrollaron métodos de cálculo (hisab) para estos problemas. Al-Juarizmi afirma que algunos estudiosos de la escuela Hanafi hicieron uso de métodos algebraicos para resolver problemas de herencia y legados. En este contexto, podemos apreciar mejor la motivación de Al-Juarizmi citada anteriormente.

Uno podría pensar que los problemas de este tipo solo deberían involucrar aritmética, no álgebra. Resulta que los eruditos legales consideraron los problemas de manera tan generalizada que la cantidad de herencia no es una cantidad específica, más bien es una cantidad general desconocida. Por tanto, era necesario aplicar las operaciones elementales de la aritmética a una cantidad general. Esta es la esencia del álgebra: tratar una cantidad desconocida como si fuera conocida y aplicar las operaciones básicas de la aritmética para las cantidades conocidas sobre la desconocida (y al final averiguar el valor de la desconocida). Por lo tanto, fue en el campo del derecho islámico donde aparecieron en gran número los problemas que requerían manipulaciones aritméticas de lo desconocido. Cuando examinamos el Libro de testamentos en la obra de Al-Juarizmi, vemos que abordó el tema de una manera sistemática y redujo los problemas a uno de los tipos de ecuaciones algebraicas que clasificó en la primera parte del libro. El trabajo de Al-Juarizmi puede verse como una justificación teórica y una sistematización del trabajo del jurista que lo precedió.

Después de comentar la importancia de la ciencia del álgebra, nos gustaría considerar otra disciplina que se encontraba entre los campos de investigación más importantes de la civilización islámica: la astronomía.

El lugar de la astronomía en la civilización islámica y su influencia en la Europa del Renacimiento

Vemos que la mayoría de los problemas que surgieron de la práctica de las obligaciones religiosas en el Islam están relacionados con la astronomía. Por lo tanto, rápidamente se convirtió en un importante campo de estudio en la civilización islámica. La astronomía es una ciencia altamente matemática y está particularmente relacionada con la trigonometría. Antes de las contribuciones de los estudiosos de la civilización islámica, la trigonometría no estaba lo suficientemente desarrollada y no se consideraba un campo por derecho propio. Los eruditos islámicos medievales contribuyeron tanto al campo de la trigonometría que alcanzó su madurez en ese período y se estableció como una disciplina por derecho propio. Quizás la mayor parte del crédito a este respecto debería ir al erudito del siglo XIII Nasir al-Din al-Tusi (Nasr, 1970). Según Berggren, el libro de Tusi The Complete Quadrilateral es el primer texto sistemático de trigonometría, independiente de la astronomía (Berggren, 2007). Un aspecto de la astronomía en la civilización islámica fue la separación de la astrología de la astronomía (Saliba 2007). La astronomía griega llegó al mundo islámico mezclada con la astrología. Sin embargo, la astrología no fue aprobada como disciplina legítima por las autoridades religiosas. Por lo tanto, los estudiosos que trabajan en el campo separaron la astrología de la astronomía, es decir, calcularían las posiciones de los cuerpos celestes pero se abstendrían de comentar sus efectos en la vida o el comportamiento humanos.

Como resultado de la importancia de la astronomía para el Islam, la institución del observatorio nació y se desarrolló en la civilización islámica (Berggren, 2003). Es uno de los legados de la ciencia islámica medieval. Un observatorio particularmente importante en el mundo islámico fue el célebre observatorio Maragha (Sayili 1960, capítulo 6) que se estableció en 1259 bajo el patrocinio de Ilkhan Hulagu, un año después de que invadiera Bagdad. Fue Nasir al-Din al-Tusi quien convenció a Hulagu para que lo estableciera. Tusi se convirtió en el director del observatorio. Fue considerado como el mejor observatorio de su época. No solo sirvió de modelo para los observatorios establecidos posteriormente (como el Observatorio Ulugh Beg en Samarqand y el Observatorio Taqi al-Din en Estambul) sino que el trabajo realizado en esta institución y la tradición del programa de astronomía que se llevó a cabo allí tuvieron algunos efectos sorprendentes sobre la ciencia del Renacimiento.

Los investigadores descubrieron en la década de 1950 que algunos de los modelos astronómicos de Copérnico (muerto en 1543) son idénticos a los modelos astronómicos del erudito islámico anterior Ibn Shatir (muerto en 1375) (Roberts 1957), que era un muwaqqit en la mezquita omeya de Damasco. También descubrieron una conexión notable entre Copérnico y Tusi cuando se dieron cuenta de que el enunciado y la demostración de un teorema de geometría dados por Copérnico eran casi idénticos al teorema descubierto por primera vez por Tusi casi tres siglos antes (Hartner, 1973). Llamado teorema de la pareja de Tusi en la literatura, este teorema fue fundamental en los trabajos de los astrónomos islámicos y también fue empleado por Copérnico en sus modelos astronómicos. Estos descubrimientos generaron muchas preguntas nuevas en la historia de la ciencia, particularmente en el área de las conexiones entre la ciencia islámica medieval y la ciencia del Renacimiento que antes no se habían notado. Esto abrió la puerta a más investigaciones. Después de estudiar la astronomía islámica y la astronomía de Copérnico, Swerdlow y Nunebaugher llegaron a la conclusión de que «En un sentido muy real, Copérnico puede ser considerado, si no el último, seguramente el seguidor más destacado de la Escuela Maragha» (Swerdlow & Neugebauer, página 295). A pesar de que han pasado décadas desde que los investigadores descubrieron estas conexiones, cuando la revolución científica en el Renacimiento se discute en los planes de estudios escolares, las conexiones entre Copérnico y los eruditos islámicos anteriores casi nunca se mencionan. En consecuencia, la mayoría de la gente nunca aprende sobre la influencia de la ciencia islámica medieval en el Renacimiento.

Los eruditos como autoridades en el conocimiento religioso y las ciencias naturales

Muchos de los eruditos islámicos medievales practicaban la religión. De hecho, algunos de ellos también eran autoridades en ciencias religiosas. Por ejemplo, Ibn al-Nafis (1213-1288), quien fue la primera persona en descubrir la circulación sanguínea pulmonar (Akmal et al, 2010), también fue un abogado Shafi en ejercicio (Saliba 2007, p.187). Nasir al-Din al-Tusi (1201-1274) fue un conocido erudito ismailí y una autoridad en el pensamiento chiíta. Ibn al-Shatir (1304-1375), cuyo trabajo aparece en Copérnico, era muwaqqit (cronometrador) en la mezquita omeya de Damasco (Saliba 2007, p. 189). Incluso aquellos eruditos que no eran necesariamente autoridades religiosas al mismo tiempo, solían comenzar sus libros alabando a Dios y al profeta Muhammad. Damos dos ejemplos de esto. El primero es el comienzo del libro de álgebra de al-Juarizmi (Rashed 2009, p. 92):

Este libro ha sido compuesto por Muhammad ibn Musa al-Juarizmi. Lo empezó diciendo:

Alabado sea Dios por Sus bendiciones, de Sus alabanzas es digno. Rendir estas alabanzas, como un deber para cualquiera de Sus criaturas que lo adore, recibe el nombre de agradecimiento, que debe aumentarse y preservarse del deterioro: reconociendo Su Divinidad, haciéndose humilde ante Su Todopoderoso y postrándose ante Su Majestad. Envió a Muhammad – Dios lo bendiga y le conceda la salvación – con la profecía como su misión, después de un intervalo de tiempo sin mensajeros, cuando la verdad fue distorsionada y la verdadera religión fue aniquilada….

Al-Kashi, que vivió unos seis siglos después de que al-Juarizmi comienza su libro Miftah al-Hisab de la siguiente manera (Aydin & Hammoudi 2019, p. 19)

En el nombre de Dios, el Más Misericordioso y Compasivo. Señor, hazlo fácil, no difícil.

Alabado sea Dios, que es el único que creó las unidades y que es único en la formación de las categorías de números. Las oraciones sean sobre lo mejor de Su creación, Muhammad, el mejor de los intercesores en el Día del Juicio. Oraciones también para su familia y descendencia, los guías del camino de la salvación y la guía justa…

Un posible conflicto entre los eruditos religiosos y la ciencia: Imam Ghazali

Como ya hemos demostrado, en general no hubo un conflicto real entre las creencias religiosas y el conocimiento científico en la civilización islámica. Algunos proponen que este no fue el caso refiriéndose a la crítica de al-Ghazali (m. 1111) a los filósofos en Tahafut al-Falasifa (La incoherencia de los filósofos). Incluso afirman que este ataque fue el final de la edad de oro de la ciencia islámica. Es posible que algunas personas en el mundo musulmán hayan malinterpretado el ataque de al-Ghazali a ciertas afirmaciones de algunos filósofos al generalizar en exceso sus críticas a las ciencias naturales. Sin embargo, una mirada cercana al propósito y la metodología de al-Ghazali en Tahafut muestra que esta afirmación es infundada. Al-Ghazali afirma claramente que solo argumentará, utilizando la misma lógica como los filósofos, que los filósofos no pudieron probar sus afirmaciones, 20 en total, que son contrarias a la creencia islámica. Él dice claramente (Al-Ghazali-Marmura 2000, p. 11) “Con respecto a las ciencias matemáticas, no tiene sentido negarlas o estar en desacuerdo con ellas. Para estas reducidas en el análisis final a aritmética y geometría. En lo que respecta a las ciencias lógicas, estas se ocupan de examinar el instrumento del pensamiento en las cosas inteligibles. No hay ningún desacuerdo significativo en estos». Más tarde, el erudito andaluz Ibn Rushd (Averroes) aclaró esta cuestión diciendo que muchas de las opiniones de Al-Ghazali expresadas en Tahafut se aplican solo a la filosofía de Avicena y no a la de Aristóteles, que Averroes sostiene que es la verdadera filosofía a partir de la cual Avicena se desvió. También argumenta que el Corán pide a los musulmanes que estudien filosofía porque el estudio y la reflexión de la naturaleza aumentarían el conocimiento de una persona sobre “el Artesano” (Dios). Cita pasajes coránicos que llaman a los musulmanes a reflexionar sobre la naturaleza y los usa para presentar una fatwa (opinión legal) de que la filosofía está permitida para los musulmanes y es probablemente una obligación, al menos entre aquellos que tienen el talento para ello (Adamson, Peter. Philosophy in the Islamic World: A History of Philosophy Without Any Gaps. Oxford University Press. 2016, p181-182).

Es realmente interesante notar que las dos primeras de las 20 doctrinas de los filósofos que al-Ghazali refutó han sido resueltas por la ciencia moderna. Siguiendo a sus antepasados ​​griegos, esos filósofos musulmanes reivindicaron la preeternidad y la poseternidad del mundo. Ahora, la cosmología moderna nos da un tiempo definido para el comienzo del universo y concluye que no será eterno. Dado el hecho de que hubo una producción científica original y avanzada en el mundo musulmán mucho después de al-Ghazali (ver Saliba 2007, capítulos 1, 6 y 7), la idea popular de que al-Ghazali provocó un freno al progreso científico en el mundo islámico no se puede sostener. Esto no quiere decir que algunas personas hayan entendido mal su posición y propósito y se hayan opuesto a todas las ciencias seculares.

En resumen, podemos ver una conexión notablemente fuerte entre la fe y la práctica del Islam y las ciencias matemáticas. Incluso en las palabras de al-Ghazali, quien es considerado por algunos como la persona responsable de poner fin a la edad de oro islámica, vemos un gran respeto por las ciencias matemáticas.

 

Fuente: Muslim Heritage

 

Bibliografía

• Adamson, Peter. Philosophy in the Islamic World: A History of Philosophy Without Any Gaps. Oxford University Press. 2016.
• Akmal M., Zulkifle M., Ansari AH, Ibn Nafis- A Forgotten Genius in the Discovery of Pulmonary Blood Circulation, Heart Views. 2010 Mar-May; 11(1):26-30.
• Al-Ghazali, The Incoherence of the Philosophers, translated by Michael E. Marmura, Brigham Young University Press, Provo, Utah, 2000.
• Al-Khalili, J. Pathfinders: The golden age of Arabic science. London: Allen Lane, 2010.
• Arnold, Thomas S. Arnold and Alfred G. The Legacy of Islam, Oxford University Press, 1931
• Berggren, J. Lennart. Episodes in the Mathematics of Medieval Islam. Softcover printing. New York:
  Springer-Verlag, 2003.
• Aydin N., Hammoudi L., Al-Kāshī’s Miftāḥ al-Ḥisab, Volume I: Arithmetic: Translation and Commentary, Birkhäuser, 2019.
• Berggren, L. Lennart. “Mathematics in Medieval Islam” in The Mathematics of Egypt, Mesopotamia, China, India and Islam. A Source Book ed. Victor J. Katz. Princeton University Press, 2007.
• Dallal, Ahmad. Islam, Science and the Challenge of History. New Haven: Yale University Press, 2010
  Hartner W. Copernicus, the man, the work and its history.” Proceedings of the American Philosophical
  Society 117, no 16 (1973): 413-422
• Kennedy, E. S. The exhaustive treatise on shadows of al-Biruni, edited with translation and commentary Aleppo, Syria: Institute for the History of Arabic Science, University of Aleppo, 1976
• King, A. David. In synchrony with the heavens : studies in astronomical timekeeping and instrumentation
  in Medieval Islamic civilization, Leiden; Boston: Brill, 2004
• Nasr S. H., Biography in Dictionary of Scientific Biography (New York 1970-1990)
• Rashed, Roshdi. Al-Khwarizmi: The Beginnings of Algebra, edited with translation and commentary.
  London: Saqi 2009.
• Robert. Victor. “The Solar and Lunar Theory of Ibn al-Shatir: A pre-Copernican Copernican Model” Isis 48 (1957)
• Saliba, George. Islamic Science and the Making of the European Renaissance. Cambridge, London. The MIT Press 2007.
• Sayili, Aydin. The observatory in Islam and its place in the general history of the observatory. Ankara Türk Tarih Kurumu Basimevi, 1960.
• Swerdlow N. M, Neugebauer O. Mathematical astronomy in Copernicus’s De revolutionibus New York: Springer-Verlag, 1984.